Research¶
Causal Models in the Case of Infinite Variance¶
There are many reasons that the canonical linear regression calculation, Ordinary Least Squares (OLS), is so predominent in Causal Analysis. To name just a few of the reasons ...
- Interpretability: The linear parametrization is so easy to understand that Financial Advisors know what's going on
- Closed-Form Solution: The formula is unique (if it exists!) and we can compute it in a resonable time --- O(n^3), which is a lot, but still usually faster than many models that use any form of gradient descent or boosting.
- And, when it meets the Gauss-Markov Assumptions, each \beta parameter will converge on a causal effect
However, when the model's noise is distributed with infinite variance (or close enough that it may as well be infinite), OLS no longer converges via the Central Limit Theorem. This means that confidence intervals may no longer be used effectively. See proof this claim in this post and read about statistically viable alternatives able to still perform causal analysis in this case, or download the entire paper here
Portfolio Optimization via Optimal Control¶
With constant risk tolerance, and with preferences categorized only by your portfolio's variance, it is simple to solve for the Markowitz-Optimal portfolio of longs and shorts (of just longs if you will); however, if risk tolerance is a function of time (or of any other variable, really), one can determine and minimize a cost functional (Wikipedia: Optimal Control Theory) that will find the portfolio composition that yields a minimum cost.
A few variations of cost functionals are proposed in a paper of mine exploring this topic.
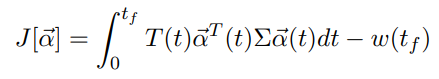
Read in more depth or download it here
Feature Selection for Causal Analysis in Stop and Frisk Dataset¶
In the Stop, Question, and Frisk Dataset, collected by NYC Police to record all street police encounters, there are over 500 possible categories that can be filled out to describe an encounter. In order to get reliable and unbiased confidence intervals for estimates in statistical models, there can be too many features, and we can bias the model by including the wrong features.
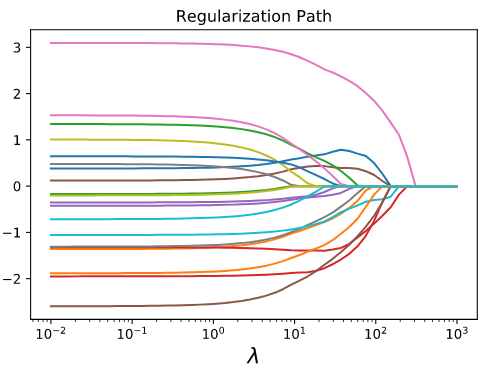
In order to algorithmically and consistently decide which features to include in a test for NYPD Racial Discrimination, I detail below in a paper how to use a Post-Double Selection LASSO model to choose parameters. After discarding all features obviously not relevant to the question of discrimination (meaning that we kept only information known by the officer before the stop), correctly using two different LASSO models can further weed out confounding erroneous factors that could deeply bias results.
The final model finds the likelihood of firearms or drugs on the person stopped, and finds that being black decreases the likelihood of possession. This implies that Blacks were not only stopped in a higher proportion to their share of the population, but that the police were not completely justified for the stops since they were less successful by their stop-rates in finding contraband among Blacks than among any other racial subpopulation.
Read more in depth or download it here
A Survey in Time-Series Weather Prediction Models¶
The canonical prediction question has always been predicting the weather: inherently random, with predictable elements we can still consider. I this paper, we survey various time-series models such as the Auto-Regressive model, the Auto-Regressive Moving-Average model, Recurrent Neural Networks, and RNN-LSTMs
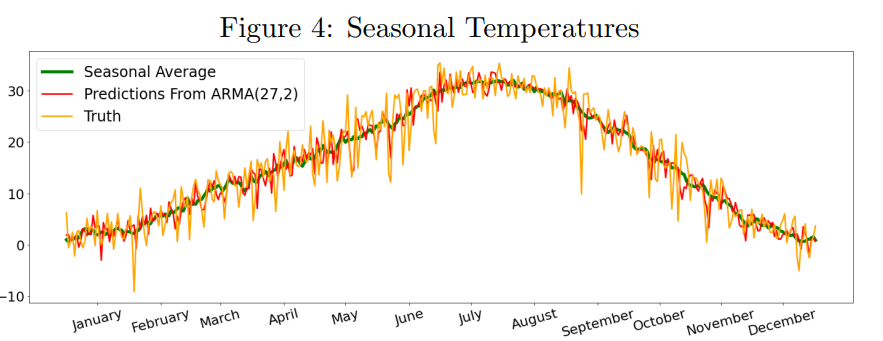
We find that this age-old problem is complex and is still being researched to this day by thousands of Data Scientists.
Read more in depth or download it here
Emotion Classification in Audio¶
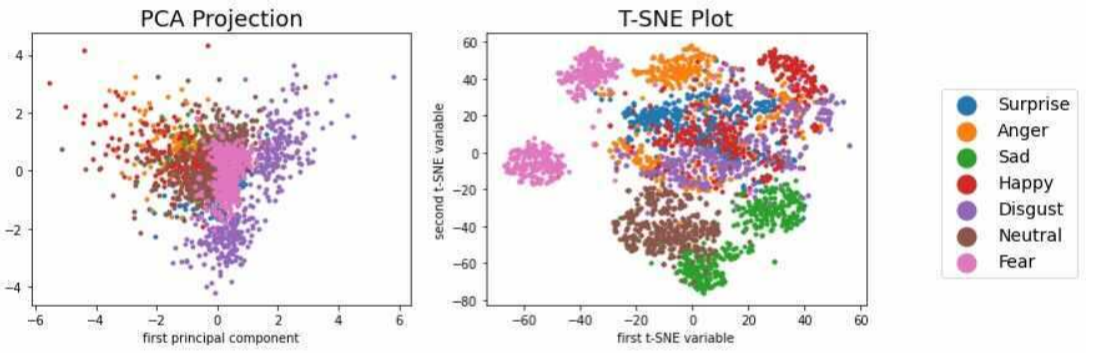
What if your voice assistant could detect your emotion behind your words? Sarcasm even? In a research paper, we test the feasibility for AI to learn to recognise emotion, learn how generalizable emotion detection can be, and what problems or ethical concerns may stand in the way.
Gradient-Boosted Trees, Random Forests, and Logistic Regressions are used to specify an accurate model that can detect any of 7 emotions: Surprise, Anger, Sadness, Happiness, Disgust, Fear, and Neutral (the absence of emotion).
Read more in depth or download it here
The Effect of No-Fault Insurance on Auto Insurance Premiums¶
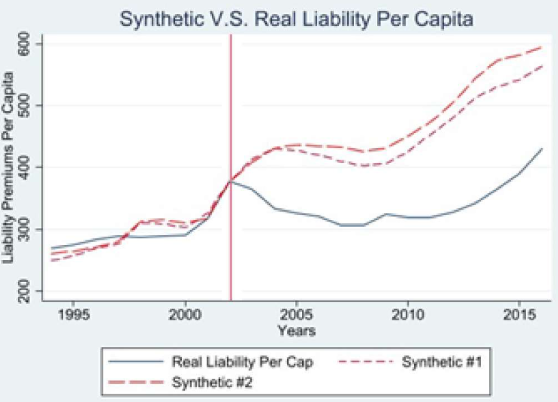
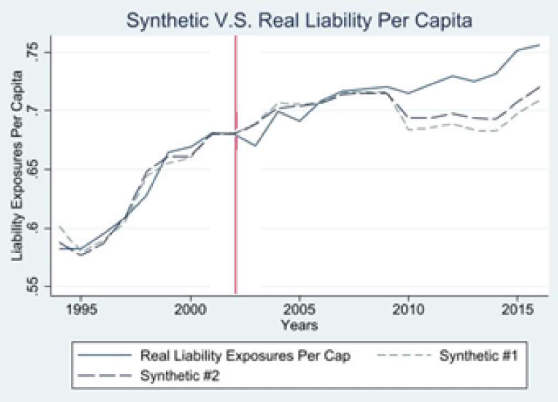
No-Fault insurance, often referred to as Personal Injury Protection (PIP) Coverage, is often legislated by states in the United States as a required coverage for motorists to cover potential damages and costs incurred, accessible regardless of driver fault.
In 2003, Colorado voters decided to remove the No-Fault mandate from the books. Using a statistical method of creating a couterfactual called Synthetic Control, after some assumptions we can estimate a Synthetic Colorado, where No-Fault was never voted away. Using this method, and checking various statistical tests, we see that it is quite possile that the pivot away from No-Fault lowered liability and collision premiums while also increasing the number of insured vehicles on the road: lowering costs, and enfranchising new drivers.